
Todo empezó con una antigua leyenda.
Según una conocida leyenda, al norte de la antigua India vivió un monarca, llamado Iadava, que se tuvo que enfrentar con su ejército a Varangul, un tirano que había lanzado un ataque para conquistar las pacíficas tierras del rey. Para derrotar a su enemigo, Iadava tuvo que sacrificar muchas vidas durante la batalla, incluso la de su propio hijo. Pese al gran logro militar, el rey quedó embargado en una profunda tristeza por la muerte de su heredero.
Un tiempo después, un joven clérigo llamado Sessa pidió audiencia ante Iadava para obsequiarle con un juego que había inventado con el que estaba seguro que podría ayudarle a aliviar su dolor.
Le entregó un tablero cuadrado, con una cuadrícula formada por sesenta y cuatro casillas, y dos conjuntos de piezas de diversas formas, unas blancas y otras negras, que representaban dos ejércitos, con todos sus regimientos y el rey a la cabeza. Tras enseñarle las reglas y los movimientos de esas piezas, Iadava comenzó a jugar con sus cortesanos. Pronto entendió que para vencer a ese juego que simulaba la guerra era necesario sacrificar varios regimientos o incluso la vida de hombres nobles, exactamente lo que le pasó a él con la vida de su hijo. En ese preciso momento, el gran tormento que le acompañaba desapareció de su corazón.
El rey quedó tan agradecido por ese inesperado regalo que le dijo a Sessa que le pidiera lo que él quisiera en recompensa. Sessa pidió unos simples granos de trigo: un grano por la primera casilla del tablero, dos granos por la segunda, cuatro por la tercera, ocho por la cuarta, y así sucesivamente, duplicando los granos de trigo, hasta completar las sesenta y cuatro casillas del juego. Muy controvertido por la extraña solicitud y por la pequeñez de lo pedido, Iadava ordenó que los sabios de la corte calculasen la deuda contraída con Sessa y que el trigo le fuera entregado de inmediato.
Tras largo tiempo calculando, los sabios comunicaron al monarca que la cantidad de trigo solicitada por Sessa simplemente era inconcebible para la imaginación humana, no existiendo suficientes tierras en el mundo para cultivarla. Dada la imposibilidad de lo pedido y como muestra de lealtad a su rey, Sessa renunció a su recompensa (también he oído que le ejecutaron allí mismo).
Había nacido el ajedrez. (Fuente: “El hombre que calculaba”. Malba Tahan)
Números que ni te imaginarías…
Pero, ¿cuánto trigo pidió Sessa? Aunque a primera vista parece que su premio no eran más que unos pocos sacos de cereal, la verdad es muy diferente: echando números, salen aproximadamente 18 trillones de granos de trigo.
Nº de granos de trigo en cada casilla
Pequeña ayuda matemática :
x103: Miles
x106: Millones
x109: Miles de millones
x1012: Billones
x1015: Miles de billones
x1018: Trillones
Gran ayuda matemática:
En cada casilla hay el mismo número de granos que la suma de todas las anteriores menos uno.
Curiosidad Matemática:
Si dividimos 1 entre 98, obtenemos el número 0,010204081632… Si nos fijamos bien, los decimales representan de forma ordenada los granos de trigo de cada casilla.
Como en un kilo hay más o menos 24.000 granos de trigo, Sessa pidió unas 768.000 millones de toneladas de cereal. La FAO estima que la producción mundial de trigo de la cosecha 2017/18 será de casi 750 millones de toneladas. Es decir, la deuda que Iadava contrajo equivalía a unos mil años de la producción actual mundial de trigo, sin duda la mayor de la historia.
Alcanzando el límite de lo racional.
La mente humana está acostumbrada a pensar en las primeras casillas el tablero de ajedrez, donde las cosas son más o menos proporcionales entre sí, donde siempre podemos encontrar una referencia con la que comparar: esta casa vale el doble ahora que hace unos años, ese profesor es cien veces mejor… En cambio no estamos acostumbrados a hablar en términos de cambios exponenciales.
En 1965, el cofundador de Intel, Gordon Moore, dijo en referencia a cómo iba a evolucionar la tecnología en el futuro que “el número de transistores por unidad de superficie en circuitos integrados se duplicaría cada año”, es decir, traduciendo, que la potencia o velocidad de los ordenador se duplicaría año a año, lo que empezó a conocerse como Ley de Moore. Sin embargo, sólo diez años después tuvo que modificarla, pasando de uno a dos años la frecuencia de la duplicación. En 2007, el propio Moore vaticinó que su ley dejaría de cumplirse en poco más de diez años.
Si alguien pudo comprobar de primera mano esta predicción fue el campeón del mundo de ajedrez Gary Kasparov, quien en 1996 se enfrentó en una inolvidable partida a Deep Blue, un superordenador desarrollado por IBM para jugar al ajedrez. De las 6 partidas del encuentro, el ruso ganó tres veces, mientras que la máquina solo pudo hacerlo en una ocasión, quedando el resto en tablas, con un cómputo final de 4 a 2 para Kasparov. Pero IBM quiso la revancha: solo un año después, en 1997, presentó una nueva versión de Deep Blue que podía calcular 200 millones de posiciones por segundo, el doble que el año anterior. En esta ocasión, Kasparov solo fue capaz de ganar una de las seis partidas, acabando el marcador en 3,5 a 2,5 a favor de Deep Blue. La máquina había vencido al hombre.
El ritmo de la evolución tecnológica es vertiginoso.
Para comprobar el ritmo vertiginoso de la innovación tecnológica no hay que irse muy lejos: la velocidad de computación de cualquier smartphone de los que llevamos en nuestros bolsillos es mayor que la de Deep Blue. Casi da miedo pensarlo.
La segunda mitad del tablero de ajedrez. La hora de soñar.
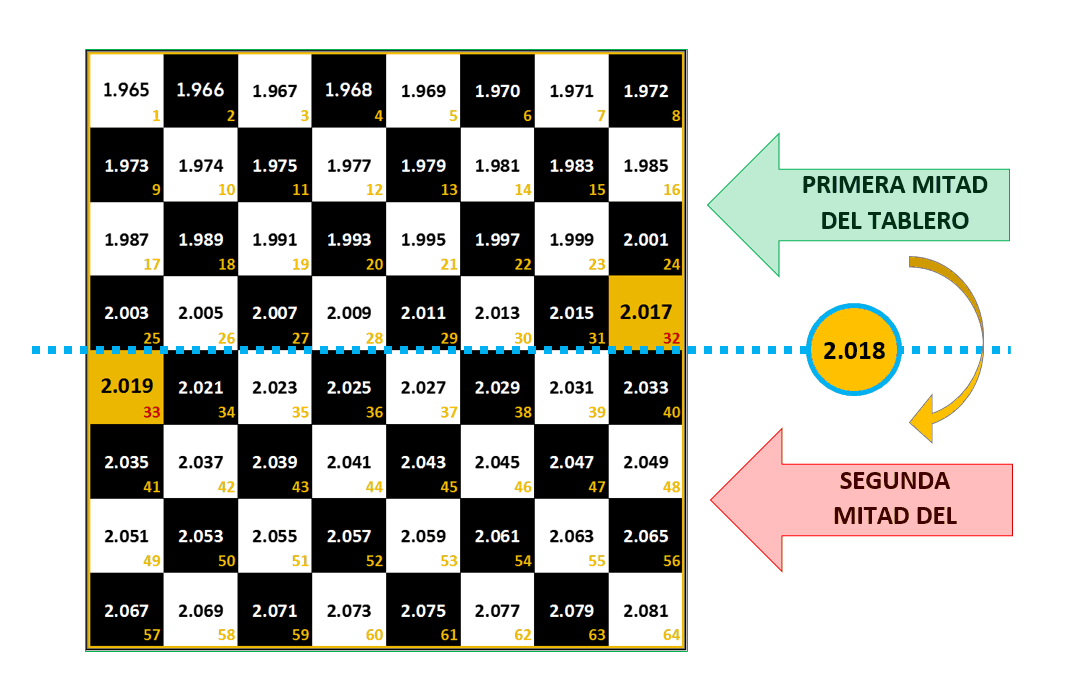
En la primera mitad de nuestro tablero de ajedrez las cifras van siendo cada vez más elevadas, muy elevadas, pero siguen estando dentro de lo razonable. Pero cuando se salta de la casilla 32 a la casilla 33 y se pasa a la segunda mitad del tablero todo cambia: las cifras empiezan a escaparse de lo concebible, los crecimientos son tan rápidos que pueden hacerse inimaginables. Los granos de trigo de la primera mitad del tablero caben en 30 camiones, absolutamente insignificante si lo comparamos con las ingentes cantidades de la segunda.
Si trasladamos la Ley de Moore a un tablero de ajedrez, colocando en la primera casilla el año 1965, cuando fue enunciada, vemos que el año 2017 está en la casilla 32 y el año 2019 en la 33. Es decir, virtualmente estamos pasando a la segunda mitad del tablero de ajedrez, donde el avance tecnológico será tan vertiginoso y las innovaciones tan comunes que nos parecerán lo cotidiano.
2018 marca la frontera entre lo posible y lo increíble.
Hasta ahora el número de chips de los que hablaba Moore ha ido aumentando tal y como él decía, pero a la vez su tamaño se ha ido reduciendo necesariamente (microchips, nanochips…) hasta tal punto que estamos llegado al “límite físico de la miniaturización” y por tanto a lo que ya predijo: la muerte de su ley. Para continuar con el mismo ritmo de crecimiento tecnológico que existe hoy, tienen que aparecer necesariamente otras nuevas tecnologías que complementen y luego sustituyan las actuales. Puede que la respuesta sea la creación de chips cuánticos, noticia que apareció hace pocos días en el diario ABC.
Estamos al límite de la Ley de Moore, cruzando a la mágica segunda mitad del tablero de ajedrez, donde nuestro conocimiento, curiosidad y creatividad nos llevarán a innovar cada vez más y más rápido, donde lo razonable dejará paso a lo casi impensable, a lo inimaginable: internet de las cosas, inteligencia artificial, computación cognitiva, digitalización de los átomos…
Entramos en la segunda mitad del tablero de ajedrez. Soñemos el futuro; puede que se haga realidad.

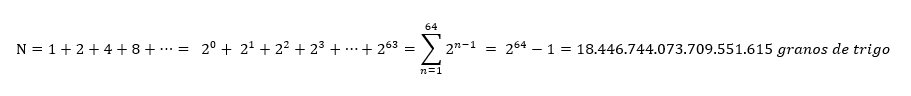






Todavía no hay comentarios