
It all starts with an old story…
Legend has it that there was an old king in the north of India called Iadava whose army fought against Varangul, a tyrant who launched an attack on the king’s peaceful kingdom in an attempt to conquer it. To defeat the enemy, Iadava had to sacrifice many lives in battle, including that of his own son. Despite his great military victory, the king sunk into a state of immense sadness over the death of his beloved heir.
Some time later, a young brahmin named Sessa asked to see Iadava, claiming he had for him a game he had invented and which he was sure would help alleviate his suffering.
Sessa gave the king a board divided into sixty-four squares, and two sets of figures of various shapes, one set white, the other black, representing two armies, with their regiments and their king at the head. After being shown the rules of the game and the way each piece could move, Iadava started to play with his courtiers. He soon learned that, in order to win at the game, which simulated a war, it was necessary to sacrifice several regiments, or even the lives of noble men, exactly as had happened with the life of his son. And realising this, the anguish which had enveloped him vanished from his heart.
The king was so grateful for this unexpected gift that he asked Sessa what he wanted as a reward. Sessa asked only for a few grains of wheat: a grain of wheat for the first square on the board, two for the second, four for the third, eight for the fourth, and so on, multiplying the number of grains by two for every square until he reach number 64. Bewildered by this strange request and the seemingly scarce value of the reward, Iadava ordered his court advisors to calculate how much was owed to Sessa, and to pay him immediately.
After a lengthy period of calculation, the advisors told the king that the amount of wheat requested by Sessa was simply unimaginable for the human mind, and that there would not be enough land in the world to cultivate it. Given the impossibility of what he had asked for, and as proof of his loyalty to the king, Sessa waived his reward (although some versions say that he was executed there and then).
And that is how the game of chess was born. (Source: “The man who counted”. Malba Tahan)
Numbers you can’t even imagine…
So how much wheat did Sessa actually ask for? Although it might at first appear that the reward requested was but a few sacks of grain, the reality is quite different. When calculated, the amount is something like 18 quintillion grains of wheat.
Grains of wheat per square
A little mathematical help:
x103: thousands
x106: millions
x109: billions
x1012: trillions
x1015: quadrillions
x1018: quintillions
More mathematical help:
The number of grains in each square is the sum of the grains in all the preceding squares minus one.
Mathematical curiosity:
If you divide 1 by 98, the result is 0,010204081632… where the decimals represent the grains of wheat in each square in ascending order.
As there are approximately 24,000 grains of wheat per kilo, Sessa in fact asked for some 768,000 million tons of wheat. The FAO estimates that global wheat production in 2017-18 will be approximately 750 million tonnes. Which means that Iadava’s debt was equivalent to almost a thousand years’ worth of today’s wheat production, no doubt the world’s largest debt ever.
Reaching the limits of the rational
The human mind is used to thinking along the lines of the first squares on the chess board, where things are more or less proportional, where we have a reference with which to make comparisons: this house is today worth twice as much as it was some years ago; that teacher is a hundred times better… We are, however, not used to talking in exponential terms.
In 1965, Intel cofounder Gordon Moore, speaking of how technology would evolve in the future, stated that “the number of transistors per unit area in integrated circuits would double every year”, meaning that the power or speed of computers would double year on year. This came to be known as Moore’s Law. However, he had to change this only ten years later, revising his forecast to a doubling every two years. In 2007, Moore himself calculated that his law would stop holding true in ten years or so.
If there was anyone capable of testing this prediction first-hand, it was world chess champion Gary Kasparov, who in 1996 played an epic match against Deep Blue, a chess supercomputer developed by IBM. Of the six games in the match, the Russian won three times, the machine only once, and the others ended in a draw, with the overall result being 4-2 for Kasparov. But IBM wanted a rematch, and just a year later, in 1997, they came up with a new version of Deep Blue which could calculate 200 million positions per second, twice the number of the previous year. This time, Kasparov won only one of the six games, with the overall result being 3,5 to 2,5 for Deep Blue. Man had been beaten by the machine.
The pace of technological evolution is dizzying.
Evidence of this dizzying pace of technological innovation is close to hand: the computing speed and capacity of any smartphone we carry around with us today is greater than that of Deep Blue. It’s almost frightening to think about.
The second half of the chessboard. Time to dream
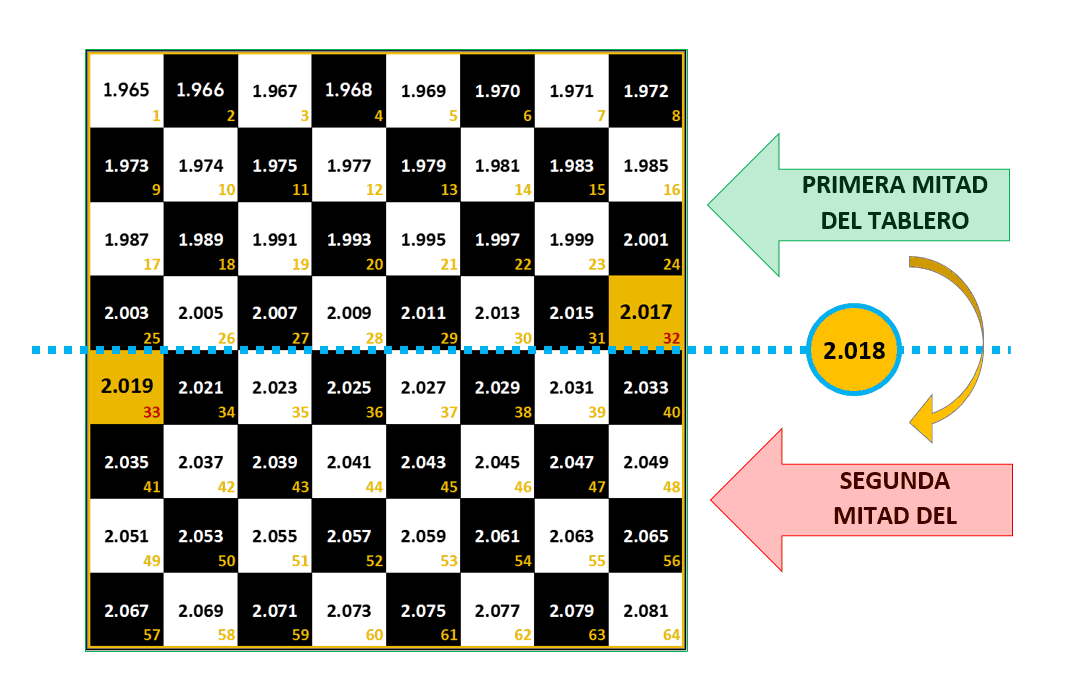
On the first half of our chessboard, the numbers grow steadily and become fairly large, but they stay within the realms of the rational. But when we go from square 32 to 33 and get to the second half of the board, everything changes: the numbers start to become hard to grasp, growing so rapidly that they become unimaginable. The grains of wheat from the first half of the board fit into 30 lorries, but this is an insignificant amount when compared with the vast amounts on the second half.
If we take Moore’s Law to the chessboard, putting 1965 on square one (as the year in which Moore stated his law) year 2017 falls on square 32 and 2019 on square 33. In other words, we are virtually now stepping onto the second half of the chessboard, where technological advances will be so rapid and innovations so frequent that we will see them as an everyday occurrence.
2018 marks the limit between the possible and the incredible.
Up to now, the number of chips as referred to by Moore has grown as predicted, though at the same time their size has decreased (microchips, nanochips…) to such an extent that we are fast approaching the “physical limits of miniaturisation” and therefore, as he also predicted, to the obsolescence of his law. For today’s pace of technological growth to continue, new technologies must necessarily emerge to complement and eventually take over our current ones. Perhaps through the creation of quantum chips, as argued in a recently published article in the Spanish newspaper ABC.
We are at the limits of Moore’s Law, crossing into the magical second half of the chessboard, where our knowledge, curiosity and creativity will lead us to ever more rapid innovation, where the rational will make way for the unthinkable and then the unimaginable: the internet of things, artificial intelligence, cognitive computing, digitalisation of atoms…
We’re stepping onto the second half of the chessboard. Let’s dream the future: and perhaps it will come true.

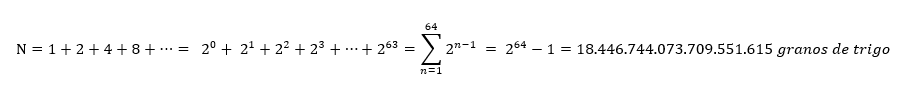







There are no comments yet